Apa itu Running Time dan Big O notation?

Lanjutan dari tulisan saya yang kemarin Belajar Algoritma Binary Search. Hari ini saya mau belajar Running Time dan Big O Notation. Okee langsung aja.

Running Time

Setiap berbicara tentang algoritma, kita tidak akan jauh dengan yang namanya running time atau waktu eksekusi sebuah algoritma. Secara umum, kita pasti ingin memilih algoritma yang paling efisien, entah kita perlu mengoptimasi waktu atau ruang (memori).

Balik ke binary search, berapa banyak waktu yang kita hemat dengan menggunakannya? Dengan pendekatan pertama yang dimana harus mengecek setiap angka nya satu persatu. Jika list elemen angkanya ada 100, kita perlu mengecek juga 100 kali. Jika list elemen angkanya ada 4 miliar, kita juga perlu mengecek 4 miliar kali. Jadi maksimal jumlah pengecekan sama dengan jumlah ukuran list yang ada. Ini disebut linear time

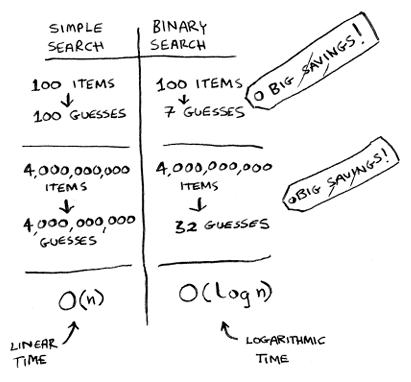
Nah berbeda dengan binary search, jika ukuran list nya ada 100, kita hanya perlu melakukan pengecekan 7 kali paling banyak. Jika ukuran list nya ada 4 miliar, paling banyak pengecekannya adalah 32 kali. Mantab kan bedanya jauh banget sama simple search. Binary search berjalan dalam logarithmic time atau log time. Berikut gambaran waktu eksekusi untuk algoritma pencarian. Run times for search algorithms

Big O notation

notasi Big O adalah notasi spesial yang mengatakan atau mengekspresikan seberapa cepat sebuah algoritma. Yaa sebenarnya penting gak penting yaa, tapi jika kita seringnya pakai algoritma orang lain, bagus untuk mengetahui seberapa cepat atau lambat algoritma tersebut.

Algorithm running times grow at different rates

Bob sedang menulis algoritma pencarian untuk NASA. Algoritmanya akan aktif ketika roket mau mendarat di bulan, dan akan membantu menghitung lokasi pendaratan.

Ini adalah contoh bagaimana waktu eksekusi dua algoritma bisa bertumbuh pada tingkatan yang berbeda. Bob masih bingung mau pilih antara simple search atau binary search. Algoritmanya harus cepat dan tepat. Di sisi lain, binary search tentu lebih cepat. Dan Bob hanya punya waktu 10 detik untuk menentukan lokasi pendaratan, jika tidak, roket akan melenceng. Di sisi lain, simple search lebih mudah untuk ditulis, dan kemungkinan munculnya bug lebih kecil. Dan Bob sangat ingin kode nya tidak ada bug untuk mendaratkan roket. Agar lebih berhati-hati, Bob memutuskan untuk mengatur waktu kedua algoritma dengan list berisi 100 elemen.

Kita asumsikan perlu waktu 1 ms (milisecond) untuk mengecek 1 elemen. Dengan simple search, Bob perlu mengecek 100 elemen, jadi pencariannya perlu waktu 100 ms. Di sisi lain, dia perlu mengecek 7 elemen dengan binary search (log₂ 100 kira-kira 7), jadi pencariannya perlu waktu 7 ms. Tapi realita nya, list nya kurang lebih ada 1 miliar elemen. Jika seperti itu, berapa lama waktu yang diperlukan untuk simple search? Berapa lama waktu yang diperlukan untuk binary search? Pastikan kamu punya jawabannya sebelum melanjutkan baca. 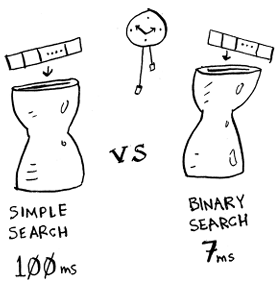Running time for simple search vs binary search with a list of 100 elements

Bob menjalankan binary search dengan 1 miliar elemen, dan perlu waktu 30 ms (log₂ 1.000.000.000 kira-kira 30). "Wohh 30 miliseconds!" dia pikir. "Binary search 15 kali lebih cepat daripada simple search karena simple search perlu 100 ms dengan 100 elemen, dan binary search perlu 7 ms. Jadi simple search akan perlu 30 x 15 = 450 ms, kan? masih jauhlah yaa dari threshold atau ambang batas 10 detik." Bob memutuskan untuk pakai simple search. Apakah itu pilihan yang benar?

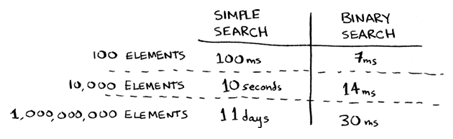
Tidak. Ternyata Bob salah. Salah Besar. Waktu eksekusi untuk simple search dengan 1 miliar elemen perlu waktu 1 miliar ms, yang berarti 11 hari! Masalahnya, waktu eksekusi untuk binary search dan simple search don't grow at the same rate atau tidak tumbuh pada tingkatan yang sama. Run times grow at very different speeds!

Berarti, seiring bertambahnya jumlah item atau elemen, binary search membutuhkan waktu yang sedikit lebih lama untuk dijalankan. Namun simple search butuh waktu yang jauh lebih lama. Jadi, seiring bertambahnya jumlah elemen, binary search tiba-tiba menjadi jauh lebih cepat daripada simple search. Bob mengira binary search 15 kali lebih cepat daripada simple search, tapi itu salah. Itulah mengapa tidak cukup hanya mengetahui berapa lama waktu yang dibutuhkan suatu algoritma untuk berjalan, Kita perlu tahu bagaimana waktu eksekusi bertambah seiring bertambahnya ukuran elemen pada list. Nah, di situlah notasi Big O berperan.

notasi Big O mengatakan seberapa cepat sebuah algoritma. Contohnya, misal kita punya list dengan ukuran n. Simple search perlu mengecek setiap elemen, jadi perlu waktu eksekusi n operasi. Waktu eksekusi notasi Big O adalah O(n). Dimana detiknya? Tidak ada. Big O tidak mengatakan kecepatan dalam detik. Notasi Big O memungkinkan kita untuk membadingkan jumlah operasi, memberi tahu kita seberapa cepat algoritma berkembang.

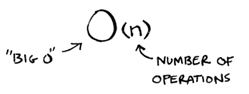
Binary search perlu log n operasi untuk mengecek sebuah list dengan ukuran n. Berapa waktu eksekusinya dalam notasi Big O? Jawabannya adalah O(log n). Secara umum, notasi Big O dituliskan sebagai berikut. Big O notation

Notasi ini memberi tahu kita berapa banyak operasi yang akan dilakukan sebuah algoritma. Disebut notasi Big O karena kita menaruh huruf "O besar" di depan jumlah operasi.

Visualizing different big O run times

Berikut contoh praktis yang bisa kamu ikuti di rumah dengan beberapa lembar kertas dan pensil. Misalkan kamu perlu menggambar kotak-kotak sejumlah 16 kotak.

Algoritma 1

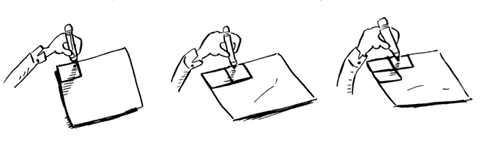
Salah satu caranya adalah menggambar 16 kotak, satu per satu. Ingat, notasi Big O menghitung jumlah operasi. Dalam contoh ini, menggambar satu kotak sama dengan satu operasi. Kamu harus menggambar 16 kotak. Berapa jumlah operasi yang diperlukan untuk menggambar satu kotak dalam satu waktu? Drawing a grid one box at a time

Perlu 16 langkah untuk menggambar 16 kotak. Berapa waktu eksekusi untuk algoritma ini?

Algoritma 2

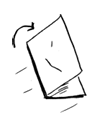
Coba algoritma ini sebagai gantinya. Lipat kertasnya. Fold the paper

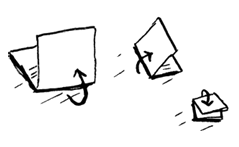
Dalam contoh ini, tiap lipatan kertas sama dengan satu operasi. Kamu telah membuat dua kotak dengan operasi tersebut. Lipat kertasnya lagi, lagi, dan lagi. Fold the paper again, and again, and again

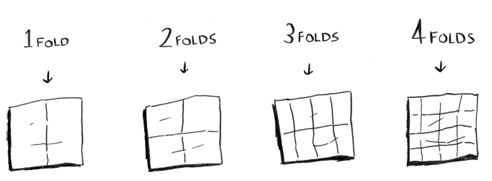
Buka lipatannya setelah empat kali lipatan, dan kamu akan mendapatkan kotak yang bagus! Setiap lipatan menggandakan jumlah kotak. Kamu telah membuat 16 kotak dengan empat operasi! Drawing a grid in four folds

Kamu dapat "menggambar" kotak dua kali lebih banyak setiap kali dilipat. Berapa waktu eksekusi untuk algoritma ini?

Jawabannya: Algoritma 1 membutuhkan waktu O(n), dan algoritma 2 membutuhkan waktu O(log n).

Big O establishes a worst-case run time

Misal kamu menggunakan simple search untuk mencari seseorang di buku telepon. Kamu tahu bahwa simple search perlu waktu O(n) untuk berjalan, yang berarti, dalam kasus terburuk, kamu harus mencari seluruh item atau elemen di buku teleponmu. Dalam kasus ini, kamu mencari Adit. Orang ini ada di daftar pertama di buku teleponmu. Jadi kamu tidak perlu mencari setiap daftar atau elemen, karena kamu menemukannya pada percobaan pertama. Apakah algoritma ini membutuhkan waktu O(n) atau O(1) karena kamu menemukan namanya pada percobaan pertama?

Simple search masih membutuhkan waktu O(n). Dalam kasus ini, kamu menemukan apa yang kamu cari secara instan. Itu skenario terbaiknya. Tapi kita menggunakan notasi Big O untuk analisa skenario terburuk. Jadi kamu bisa mengatakan bahwa skenario terburuknya, kamu harus mencari seluruh daftar nama di buku telepon sekali. Itulah waktu O(n). Ini bisa dianggap sebagai sebuah kepastian, kamu tahu bahwa pencarian sederhana tidak akan pernah lebih lambat dari waktu O(n).

Catatan

Selain waktu eksekusi skenario terburuk, penting juga untuk melihat waktu eksekusi skenario rata-rata. Perbedaan antara skenario terburuk dan skenario rata-rata akan dibahas di tulisan selanjutnya.

Some common big O run times

Berikut 5 waktu eksekusi big O yang bakal sering kamu temui, diurutkan dari tercepat hingga paling lambat:

O(log n), atau dikenal juga sebagai log time. Contoh: binary search.
O(n), atau dikenal juga sebagai linear time. Contoh: simple search.
O(n * log n). Contoh: sebuah algoritma pengurutan cepat, seperti quicksort.
O(n²). Contoh: sebuah algoritma pengurutan lambat, seperti selection sort.
O(n!). Contoh: sebuah algoritma yang paling lambat, seperti traveling salesperson.

Misal kamu menggambar 16 kotak lagi, dan kamu memilih dari 5 algoritma yang berbeda-beda untuk melakukannya. Jika kamu menggunakan algoritma pertama, itu membutuhkan waktu O(log n) untuk menggambar kotak. Kamu bisa melakukan 10 operasi per detik. Dengan waktu eksekusi O(log n), kamu membutuhkan 4 operasi untuk menggambar sebuah kotak dari 16 kotak (log 16 adalah 4). Jadi kamu membutuhkan waktu 0.4 detik untuk menggambar kotak. Bagaimana jika kamu perlu menggambar 1,024 kotak? Itu akan membutuhkan 1,024 = 10 operasi, atau 1 detik, untuk menggambar 1,024 kotak. Perhitungan ini menggunakan algoritma pertama.

Algoritma kedua lebih lambat: membutuhkan waktu O(n). Itu akan memerlukan 16 operasi untuk menggambar 16 kotak, dan itu perlu 1,024 operasi untuk menggambar 1,024 kotak. Berapa banyak waktu tersebut dalam detik?

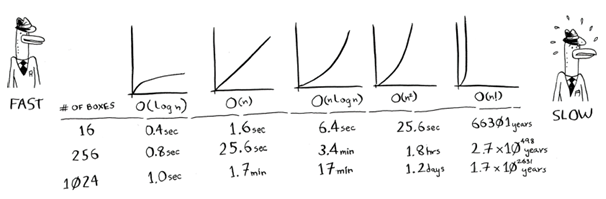
Berikut adalah berapa lama waktu yang dibutuhkan untuk menggambar sebuah kotak untuk sisa algoritma, dari tercepat hingga yang paling lambat: Time to draw a grid for each algorithms

Ada juga beberapa waktu eksekusi lainnya, tetapi berikut ini adalah lima yang paling umum.

Penjelasan ini sebenarnya adalah sebuah penyederhanaan. Pada kenyataannya, kamu tidak bisa mengubah waktu eksekusi dalam notasi Big O menjadi jumlah operasi secara rapi seperti ini. Namun, untuk saat ini penjelasan ini sudah cukup. Untuk saat ini, hal-hal utama yang perlu diingat adalah sebagai berikut:

Kecepatan algoritma tidak diukur dalam detik, melainkan dalam pertumbuhan jumlah operasi.
Alih-alih menghitung dalam detik, kita membicarakan seberapa cepat waktu eksekusi algoritma bertambah ketika ukuran input bertambah.
Waktu eksekusi algoritma dinyatakan dalam notasi Big O.
O(log n) lebih cepat daripada O(n), dan perbedaannya akan menjadi jauh lebih cepat seiring ukuran list yang dicari semakin besar.

dah gitu dulu yaa~